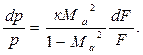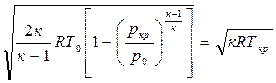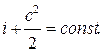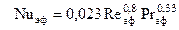что такое температура торможения при движении газа
температура торможения
температу́ра торможе́ния потока температура Т0 изоэнтропически (без теплообмена с внешней средой) заторможенного газа. Играет важную роль при движении идеального совершенного газа; в так называемом адиабатическом течении она соответствует максимально возможной температуре газа и характеризует его полную удельную энергию, которая остаётся постоянной вдоль линии тока. При отсутствии массовых сил её значение вычисляется на основе Бернулли уравнения:
где Т температура, V скорость, cp удельная теплоёмкость газа при постоянном давлении. Часто используется в аэродинамических расчётах в качестве характерного масштаба температуры.
Смотреть что такое «температура торможения» в других словарях:
температура торможения — температура заторможенного потока; температура торможения Температура, соответствующая энтальпии заторможенного (остановленного) потока. Температура в рассматриваемой точке потока газа при предположении адиабатного торможения газа в этой точке до … Политехнический терминологический толковый словарь
температура торможения — (To) Температура изоэнтропически заторможенного газа. [ГОСТ 23281 78] Тематики аэродинамика летательных аппаратов Обобщающие термины характеристики течения газа EN stagnation temperature … Справочник технического переводчика
температура торможения — 3.2 температура торможения: Температура движущейся среды, учитывающая увеличение среды при полной остановке потока. Источник: ГОСТ Р ЕН 306 2011: Теплообменники. Измерения и точность измерений при определении мощности … Словарь-справочник терминов нормативно-технической документации
температура торможения — stabdymo temperatūra statusas T sritis Energetika apibrėžtis Didelio greičio dujų srauto charakteristika. Stabdymo temperatūros skaitinė vertė – dujų srauto temperatūra, kai jo greitis sumažinamas iki nulinio, vykstant izoentropiniam procesui.… … Aiškinamasis šiluminės ir branduolinės technikos terminų žodynas
температура торможения — потока температура Т0 изоэнтропически (без теплообмена с внешней средой) заторможенного газа. Играет важную роль при движении идеального совершенного газа; в так называемом адиабатическом течении она соответствует максимально возможной… … Энциклопедия «Авиация»
ТЕМПЕРАТУРА ТОРМОЖЕНИЯ — одна из хар к высокоскоростного потока газа, равная темп ре этого газа, изоэнтропически заторможённого до нулевой скорости (см. Изоэнтропийный процесс) … Большой энциклопедический политехнический словарь
Температура торможения потока — температура Т0 изоэнтропически (без теплообмена с внешней средой) заторможенного газа. Играет важную роль при движении идеального совершенного газа; в так называемом адиабатическом течении она соответствует максимально возможной температуре газа… … Энциклопедия техники
температура торможения в абсолютном движении на входе в рабочую лопатку газовой турбины при работе в базовом режиме — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN baseload firing temperaturefiring temperature … Справочник технического переводчика
температура торможения потока — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN stagnation temperature … Справочник технического переводчика
температура торможения потока на входе — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN entrance stagnation temperature … Справочник технического переводчика
ТЕРМОДИНАМИКА ГАЗОВОГО ПОТОКА
4.1. Уравнения и параметры движущегося газа
В рассмотренных выше процессах не учитывалась кинетическая энергия рабочего тела. Однако в теплотехнике широко распространены энергетические установки, в которых преобразование энергии осуществляется в движущемся газе. Такие процессы происходят в турбинах, реактивных двигателях, лопаточных и струйных компрессорах и т.п.
Рассмотрим уравнения термодинамики для стационарного одномерного потока идеального газа.
Для газового потока в любом сечении справедливо уравнение состояния, записанное через плотность:
где p – давление в рассматриваемом сечении;
ρ – плотность газа в этом сечении;
R – газовая постоянная;
T – термодинамическая температура (температура, которую покажет в данном сечении безинерционный термометр, перемещающийся со скоро-стью газового потока).
В термодинамике величину скорости потока газа обозначают с и измеряют в м/с. Часто с целью количественной оценки величины скорости потока ее сравнивают со скоростью распространения слабых возмущений в среде газа. При выведении газа из равновесия в каком-либо месте в нем возникает движение частиц. Эти возмущения передаются по всему газу (подвижному и неподвижному) с так называемой с к о р о с т ь ю з в у к а. Скорость звука обозначается a, измеряется в м/с и вычисляется поизвестной из физики формуле:
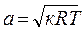
Если c 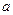
4.1.1. Уравнение энергии
В движущемся газе выделим сечениями 1-1 и 2-2, Рис. 4.1, участок потока.
На основании первого закона термодинамики для энергоизолирован- ного потока (данная система не обменивается теплотой и работой с окружающей средой) можем записать Е1 = Е2. Отсюда для m = 1кг газа уравнение (1.7) в сечениях потока будет иметь вид:
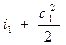
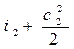
Это означает, что для любого сечения потока газа сумма энтальпии и кинетической энергии одинакова, т.е.

Выражение (4.3) называют у р а в н е н и е м э н е р г и и потока газа. Из него следует, что изменить скорость газа в потоке можно лишь только за счет изменения энтальпии.
Выражение (4.4) приписывают Д. Бернулли, поэтому в технической литературе его называют у р а в н е н и е м Б е р н у л л и.
Это уравнение устанавливает связь скорости с давлением. Из него следует, что для увеличения скорости (dc > 0) необходимо снижение давления (dp
В окончательном виде формула температуры торможения имеет вид:
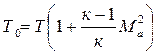
Используя адиабатную связь между температурой и давлением, получим формулу для давления торможения:
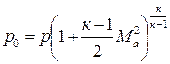
Плотность ρ0 определяется по p0 и T0 из уравнения (4.1).
4.1.3. Уравнение скорости движения газа
Уравнение скорости движения газа в произвольном сечении потока получим из уравнения энергии. Пусть газ вытекает из емкости, где его скорость была равна нулю. Тогда уравнение энергии для произвольного сечения потока газа и для сечения, где c = 0, будет иметь вид:
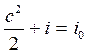
c = 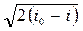
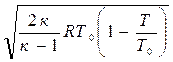
Если отношение температур заменить отношением давлений, то
c= 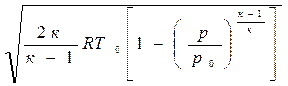
Из выражения (4.7) следует, что величина скорости газа в рассматриваемом сечении потока зависит от природы газа, от параметров в его исходном (заторможенном) состоянии и от давления газа в рассматриваемом сечении.
4.1.4. Уравнение расхода
Термодинамика газового потока в основном рассматривает стационарное движение газа. Это означает, что через все сечения канала в любой момент времени протекает одно и то же массовое количество газа. Обозначается секундный массовый расход 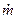

Выразим секундный массовый расход через параметры заторможенного газового потока, для чего в выражение (4.8) вместо c подставим его значение (4.7), а плотность представим в виде
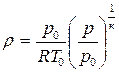
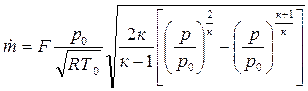
4.2. Течение газа в каналах
4.2.1. Уравнение обращения воздействия
В 1948 г. А.А. Вулис получил зависимость, выражающую связь геометрии сопла с характером внешнего воздействия на поток. Для неэнергоизолированного движения газа зависимость Вулиса имеет вид:

Здесь первое слагаемое правой части уравнения выражает г е о м е т-
р и ч е с к о е в о з д е й с т в и е на движущийся газ, второе – м а с с о в о е, третье – т е п л о в о е и четвертое – м е х а н и ч е с к о е. Уравнение (4.10) является математическим выражением принципа обращения воздействия, суть которого состоит в том, что характер влияния каждого воздействия на газовый поток противоположен при сверхзвуковых и дозвуковых течениях газа.
Проанализируем лишь геометрическое воздействие. В этом случае из уравнения (4.10) следует:
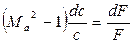

4.2.2 Течение газа в соплах Лаваля
При движении газа вдоль сверхзвукового геометрического сопла своеобразно изменяются его параметры. Для выявления характера изменения давления по длине сопла из уравнений (4.4) и (4.11) можно получит выражение:
Из анализа данного уравнения следует, что давление вдоль сопла уменьшается. Кривая давления в дозвуковой части сопла имеет выпуклый вид, а в сверхзвуковой – вогнутый. Температура вдоль сопла уменьшается, так как процесс расширения газа адиабатный. С такой же закономерностью уменьшается по длине сопла и скорость звука.
Характер изменения скорости вдоль сопла устанавливается уравнением Бернулли (4.4), записанным в виде:
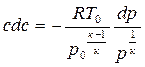

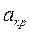
Получим выражение для ркр и Ткр через параметры торможения. В критическом сечении 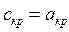
После незначительных преобра –
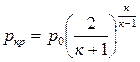
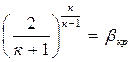
Величина β определяется только
Так, для воздуха при к = 1,4 значение βкр = 0,528. Отсюда следует, что для воздуха критическое давление меньше давления торможения в 1,89 раза.
Значение критической температуры получим из выражения (4.12), заменив отношение давлений отношением температур:
Ткр= Т0 
Теперь выражение для критической скорости можно представить в другом виде:
скр = 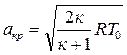
Скорость газа в каждом сечении сопла и на выходе из него вычисляется по формуле (4.7).
Если секундный массовый расход выразить через параметры торможения и площадь критического сечения, то зависимость (4.9) существенно упрощается:
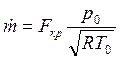
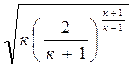
Если давление газа в выходном сечении сопла равно давлению окружающей среды ( 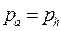
4.2.3. Дросселирование газа и пара
Д р о с с е л и р о в а н и е м называют процесс понижения давления в газовом потоке при преодолении местного сопротивления в канале.
При дросселировании газа или пара протекает необратимый процесс снижения давления без совершения внешней работы. Если в канале имеется местное сопротивление в виде резкого сужения вида перегородки с отверстием, задвижки, клапана и т.п., то газовый поток перестраивает свою геометрическую форму, как до сужения, так и после него. Перестройка формы потока и перетекание через само сужение связано с образованием вихревых движений газа. Часть кинетической энергии потока идет на образование вихрей, часть – на преодоление сопротивления трения. Затраченная на это энергия необратимо превращается в теплоту, которая воспринимается газом. Поэтому давление после местного сопротивления не восстанавливается до первоначального. Изменение давления, скорости и температуры по длине канала приведено на рис.4.4. Скорость газа при протекании его через сужение возрастает, что вызывает снижение давления и температуры. После сужения скорость понижается, но давление, вследствие указанных причин, не восстанавливается до первоначального.
Степень снижения давления газа при дросселировании зависит от природы газа и его состояния, относительной величины сужения, скорости газа. Обозначим степень снижения давления через 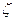

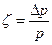
где ∆р – величина снижения давления;
р – давление на входе в сужение.
В энергетических установках дросселирование нежелательно, т.к. при падении давления снижаются энергетические возможности газа. Но иногда дросселирование является необходимым и создается искусственно, например, в редукторах, регуляторах и т.п.
При термодинамическом анализе особенностей процесса дросселирования целесообразно использовать общее уравнение энергии:
льпия газа в процессе дросселирования
остается постоянной. Рис. 4.4
Для реального газа изменение температуры при его дросселировании в отличие от идеального газа имеет своеобразный характер. Как показывают опыты, температура реального газа в результате дросселирования повышается, понижается или не изменяется. Это свойство впервые обнаружили ученые Д. Джоуль и У. Томсон, поэтому оно носит название э ф ф е к т а Д ж о у л я-Т о м с о н а.
Используя дифференциальные уравнения, связывающие i, s, ρ и T, можно получить для газа, подчиняющегося уравнению Ван-дер-Ваальса, следующую зависимость:
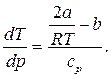
Отношение бесконечно малого изменения температуры к бесконечно малому изменению давления при дросселировании называется д р о с с е л ь—э ф ф е к т о м и обозначается
α =
Так как при дросселировании dp 0, т.е. dT 0 ( при T > 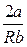
в) 
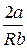
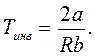
|
Понятие температуры инверсии особенно широко используется в холодильной и криогенной технике.
Каждый конкретный газ имеет индивидуальную температуру инверсии. Так, например, для воздуха Тинв = 650 К; для водорода Тинв = 204 К; для водяного пара Тинв= 682 К.

ОСОБЕННОСТИ ТЕПЛООБМЕНА ПРИ ДВИЖЕНИИ ГАЗА



С БОЛЬШОЙ СКОРОСТЬЮ
При движении газового потока с большой скоростью процессы теплообмена значительно усложняются. Это связано с тем, что в пограничном слое благодаря силам вязкости происходит резкое уменьшение скорости от максимального её значения во внешнем потоке до нуля на поверхности тела. Большие градиенты скорости поперёк пограничного слоя приводят к возникновению значительных сил трения, работа которых переходит в теплоту. В этих условиях пограничный слой можно рассматривать как малую пространственную область, в которой происходит разогрев газа за счёт диссипации кинетический энергии. Увеличение температуры газа приводит к соответствующему изменению тепловых потоков. Кроме того, большие диапазоны изменения температуры газа в пограничном слое приводят к значительным изменениям плотности, вязкости, теплопроводности и теплоёмкости теплоносителя, что также оказывает заметное влияние на интенсивность теплообмена.
Температура восстановления. Рассмотрим движение газового потока с большой скоростью вдоль пластины (рис. 2.8). Примем, что с противоположной стороны пластина теплоизолирована. Тогда на установившемся режиме ее температура станет равной температуре непосредственно прилегающих к ней слоев газа, а теплообмен между пластиной и обтекающим ее потоком будет отсутствовать.
 |
 |
| Рис. 2.8 | Рис. 2.9 |
Из-за торможения потока в пограничном слое температура газа в нем увеличивается и превышает температуру внешнего потока, увеличиваясь по мере приближения к пластине (рис. 2.8б).
Температурой восстановления Тr называется температура, которую принимает теплоизолированная (с одной стороны)пластина при обтекании её газом.
Такую же температуру будут иметь и частицы газа, непосредственно прилегающие к пластине (стенке).
Хотя частицы, прилагающие к стенке, полностью заторможены, температура восстановления оказывается несколько отличной от полной температуры набегающего газового потока. Это связано с тем, что температура восстановления зависит от двух параллельно протекающих процессов: выделения теплоты, вызванного торможением потока из-за наличия трения, и отвода теплоты в поток путём теплопроводности, возникающего из-за больших градиентов температуры по нормали к стенке в пограничном слое.
Температура восстановления определяется по формуле

Коэффициент восстановления зависит главным образом от режима течения в пограничном слое и числа Прандтля. Для продольно обтекаемой пластины при ламинарном пограничном слое r хорошо аппроксимируется формулой


Так как у газов Рr о С) значениях статической температуры теплоносителя. Этим вызывается необходимость тепловой защиты поверхностей летательных аппаратов, предназначенных для больших сверхзвуковых и гиперзвуковых скоростей полета.
Важно подчеркнуть, что при теплообмене между телом и высокоскоростным потоком газа последний может отдавать теплоту стенке даже в условиях, когда температура стенки Тст превосходит статическую температуру обтекающего её потока Тт.

Плотность теплового потока. Величина и направление теплового потока между газом и стенкой определяется не соотношением между статической температурой теплоносителя Тти температурой стенки Тст, как это имеет место при малых скоростях потока, а соотношением между температурой восстановления Тr и Тст.
Соответственно формула Ньютона для этого случая должна быть записана в виде 
При обтекании газом теплоизолированной стенки температура её поверхности равна температуре восстановления 
В приближенных расчетах можно считать, что 

Критериальные уравнения. Подобие процессов теплообмена при больших скоростях движения газа кроме критериев Re и Pr определяется также числом Маха, точнее комплексом 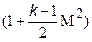


Однако в практических расчётах для определения коэффициента теплоотдачи a при больших скоростях движения теплоносителя часто используется упрощённое критериальное уравнение типа
полученное для малых скоростей, но используемое при условии, что физические параметры газа (теплоёмкость, вязкость, теплопроводность) определяются по некоторой эффективной температуре. Значение этой температуры Тэф определяется в приближенных расчетах по формуле
или по еще более простой формуле, т.е. 
Исследования показали также, что для расчета местных коэффициентов теплоотдачи при движении газа с большой скоростью в каналах переменного сечения при турбулентном течении следует для каждого сечения канала использовать следующее критериальное уравнение,
но с определением критериев подобия по эффективной температуре.
2.8. КОНВЕКТИВНЫЙ ТЕПЛООБМЕН ПРИ СВОБОДНОМ
Условия возникновения свободного движения теплоносителя. Свободным называется движение теплоносителя, возникающее вследствие различия плотностей неодинаково нагретых его объёмов. Различие плотностей приводит к неоднородному полю массовых сил (например, сил тяготения), т.е. к появлению неуравновешенных сил, действующих на частицы жидкости (газа), что обусловливает возникновение архимедовой подъемной (выталкивающей) силы, которая и вызывает свободное движение теплоносителя.
Таким образом, для возникновения свободного движения необходимо:
а) наличие массовых сил (сил тяготения, центробежных сил и др.);
б) наличие неравномерного распределения плотности теплоносителя в объеме, что имеет место при неравномерном прогреве этого объема.