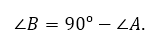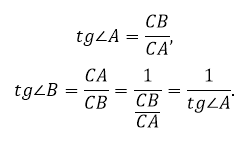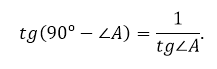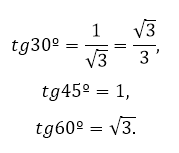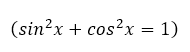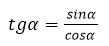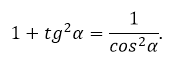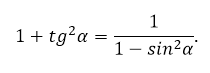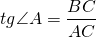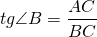что такое тангенс острого угла прямоугольного треугольника
Что такое тангенс угла и как его найти
Живущим людям на Земле
всегда хотелось знать,
как путь найти в пустыне, море,
и можно к звёздам ли попасть.
Хотелось труд свой облегчить,
создать машины, чтоб летать.
И чтоб вопросы разрешить,
пришлось про тангенс всем узнать.
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Впервые встречаясь с тригонометрией в восьмом классе на геометрии, школьники оглядываются на свою жизнь, задавая вопрос, насколько пригодится им эта область науки в дальнейшем.
Редко кто задумывается, что раздел математики, позволяющий рассказать о заданном треугольнике всё (найти все его стороны и углы, выделить особенности), позволил в своё время сделать великие открытия.
Тригонометрия, дав возможность строить корабли и самолёты, отправлять человека в космос, создавать приборы для ориентирования на море, в лесу, в пустыне, определять расстояния, не измеряя их непосредственно линейкой, шагами или чем-то иным, помогла упростить жизнь человечества, раскрыть новые горизонты знаний.
Тангенс угла
Первые встречи с тангенсом происходят при изучении прямоугольных треугольников.
В них соотношения сторон, образующих прямой угол (катетов), и стороны, лежащей напротив угла в 90º (гипотенузы), задают важные параметры для изучения углов.
Для понимания связи между объектами рассматриваются отношения различных отрезков. Задавая связь между ними, вводят понятия синуса, косинуса (это что?), тангенса, котангенса.
Важно, что это отвлечённые понятия, не связанные с какими-либо единицами измерения.
Введя функции угла, определяют их свойства. Некоторые полученные формулы могут иметь довольно громоздкий вид. Чтобы избежать затруднённого чтения, вводятся другие объекты.
Так произошло и с тангенсом. Ему посчастливилось получить два определения. Каждое характеризует заданное отношение по-своему. С одной стороны, рассматривается связь между катетами и острыми углами прямоугольного треугольника, с другой – даётся возможность упростить формулы, содержащие синусы и косинусы.
Мало кто задумывается, изучая тангенс в школе, что первоначально он был необходим, чтобы найти касательные линии к заданной кривой. Само понятие возникло от латинского слова tangens, которое означает «трогающий», «касающийся» и является причастием настоящего времени от tangere («трогать», «касаться»).
Тангенс — это отношение.
Итак, есть два определения:
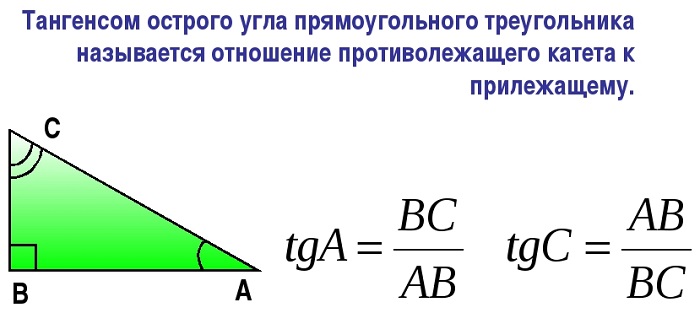
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Это определение удобно использовать при изучении геометрических фигур. Оно даёт возможность, минуя вычисления гипотенузы, находить углы или катеты. Выделяя прямоугольные треугольники в произвольных фигурах, задача по изучению свойств исследуемых объектов становится проще.
Тангенс – это отношение синуса к косинусу.
Благодаря этому определению, многие тригонометрические формулы принимают более удобный вид, становятся легче воспринимаемыми.
» alt=»»>
Вместо «тангенс угла альфа» пишут: tgα. На калькуляторах, в различных программах ЭВМ и ПК закрепилось другое обозначение: tan(α).
Как найти тангенс угла (формулы)
Первое свойство тангенса вытекает из его определения как отношения катетов.
Сумма двух непрямых углов прямоугольного треугольника равна 90º. Поэтому
Так как тангенс – это отношение катетов, то
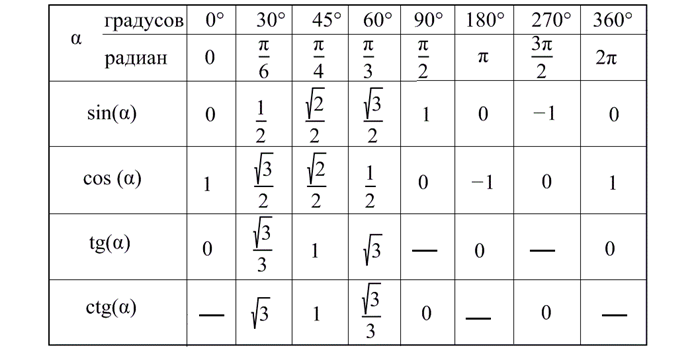
Учитывая особенности некоторых треугольников (равностороннего, прямоугольного, равнобедренного), а также записанное свойство, была составлена таблица значений тангенса для углов 30º, 45º, 60º.
Задача нахождения других углов по значению тангенса была решена с помощью составления более обширных таблиц. За счёт появления современных вычислительных средств необходимость применения табулированных значений уменьшилась.
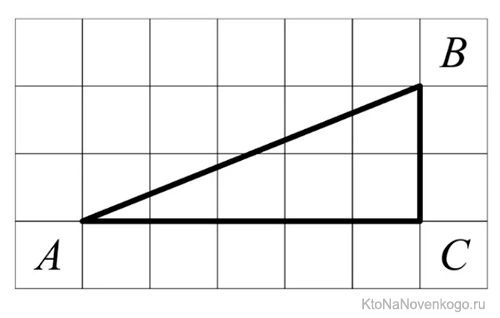
Как найти тангенс по клеточкам
Учитывая первое определение, можно определить, как найти тангенс угла по клеточкам. Рисунок дополняется перпендикулярными линиями (строится высота), затем считается количество клеточек в полученном прямоугольном треугольнике на катетах, противолежащем и прилежащем искомому углу, а затем берётся их отношение.
Благодаря второму определению, задачу, как найти тангенс угла, можно решить, минуя таблицы и построение прямоугольных треугольников. Достаточно знать синус и косинус, связанные между собой основным тригонометрическим тождеством:
Из формулы тангенсов, записывающей кратко второе определение
и основного тригонометрического тождества можно понять, как найти тангенс, зная только косинус или синус угла.
Достаточно поделить основное тригонометрическое тождество на квадрат косинуса, подставить формулу тангенса. В результате получится зависимость тангенса и косинуса:
Если выразить в последнем случае косинус, то запишется связь между тангенсом и синусом:
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (5)
Я Очень Люблю Правила, Теоремы, Формулы по Предмету «Математика», «Алгебра».
Прочитал статью и остался один главный вопрос, а собственно без вспомогательных таблиц найти угол В ГРАДУСАХ вообще возможно и есть ли у вас статья, где рассказыввается как это сделать? Спасибо.
Я ни разу не математик, но почему у вас сумма углов прямоугольного треугольника равна 90 градусов. А так все хорошо начиналось. Объясняете хорошо, но после таких ошибок у меня сомнения что информация верная.
Спасибо. Уточнил в тексте, что это сумма двух непрямых углов прямоугольного треугольника.
Пишу стихи. Востребован тангенс для решения жизненных ситуаций поскольку состоит из тех же функций,как-то, касающийся,прилежащий, трогающий. Куда без них денешься.
Тангенс в прямоугольном треугольнике
Что такое тангенс в прямоугольном треугольнике? Как найти тангенс? От чего зависит значение тангенса?
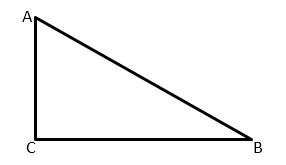
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
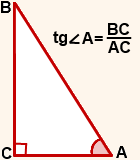
Например, для угла A треугольника ABC
Поэтому тангенс угла A в треугольнике ABC — это

противолежащим является катет AC,
Соответственно, тангенс угла B в треугольнике ABC
равен отношению AC к BC:
Таким образом, тангенс острого угла прямоугольного треугольника — это некоторое число, получаемое при делении длины противолежащего катета на длину прилежащего катета.
Так как длины катетов — положительные числа, то и тангенс острого угла прямоугольного треугольника является положительным числом.
Тангенс угла треугольника зависит от величины угла, но не зависит от катетов (важно лишь их отношение).
Если в треугольнике изменить длины катетов, не меняя угол, то величина тангенса не изменится.
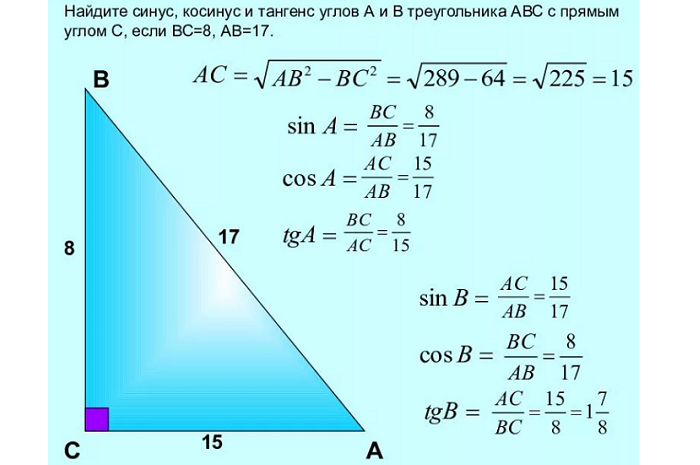
Синус, косинус и тангенс острого угла прямоугольного треугольника
Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.
Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.
Острый угол — меньший 90 градусов.
Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин 🙂
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты — стороны, лежащие напротив острых углов.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
Обратите внимание на основные соотношения для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.
Давайте докажем некоторые из них.
Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?
Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?
С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.
Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
| 0 | |
| 0 | |
| 0 | |
| 0 | − |
| − | 0 |
Обратите внимание на два красных прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.
Ты нашел то, что искал? Поделись с друзьями!
Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.
Задача решается за четыре секунды.
Найдем по теореме Пифагора.
Треугольник с углами и — равнобедренный. В нем гипотенуза в раз больше катета.
Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.
Что такое синус, косинус, тангенс и котангенс в прямоугольном треугольнике?
Синус, косинус и тангенс острого угла прямоугольного треугольника.
Приветствую Вас дорогие учащиеся.
Сейчас рассмотрим что же такое синус, косинус, тангенс и котангенс в прямоугольном треугольнике?
Это тема не сложная, главное это запомнить правила. И так начнем:
Вспомним, что такое прямоугольный треугольник?
Прямоугольным треугольником, называется треугольник у которого один из углов прямой (составляет 90 градусов). Две стороны которые прилежат к прямому углу, называются катетами, а сторона лежащая напротив прямого угла, называется гипотенузой.
Синус (sin(a)) — это отношение противолежащего катета к гипотенузе;
Косинус (cos(a)) — это отношение прилежащего катета к гипотенузе;
Тангенс (tg(a)) — это отношение противолежащего катета к прилежащему катету;
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу;
Котангенс (ctg(a)) — это отношение прилежащего катета к противолежащему.
Другое (равносильное) определение: котангенсом острого угла называется отношение косинуса угла к его синусу;
Пусть дан прямоугольный треугольник ABC с прямым углом C.


Аналогично рассуждаем относительно угла B.


Пример:
Найти тангенс угла С (tg(C)) треугольника ABC.
Хочешь готовиться к экзаменам бесплатно? Репетитор онлайн бесплатно. Без шуток. ЗДЕСЬ
Геометрические фигуры завораживают количеством своих свойств и функций, таких как тангенс в прямоугольном треугольнике. Это происходит в основном из-за двух факторов.
Во-первых, нам уже известен один из углов, который равен 90 градусам. Во-вторых, есть много свойств с применением прямоугольников. А из двух прямоугольных треугольников как раз получается именно такая фигура.
Из этого вытекает многое, но сегодня мы поговорим об одном очень интересном свойстве такого треугольника, как тангенс. В данной статье мы подробно рассмотрим определение тангенса, узнаем, как его можно найти и как его можно использовать.
Что такое тангенс в прямоугольном треугольнике
Также бывают и тригонометрические тангенсы на окружности со своими графиками, разностью показателей числа π, но в данной статье мы их не рассматриваем, так как к треугольнику они имеют лишь косвенное отношение.
Таблица тангенсов углов от 0° до 360°
Ниже представлена таблица значений, которая пригодится для быстрого нахождения необходимых значений.
В качестве альтернативы предлагаем либо искать значения онлайн, либо запоминать их. Самым же эффективным способом математики считают вывод этих значений, но это будет удобно далеко не для всех.
Примеры вычислений тангенса в прямоугольном треугольнике
Существует довольно много способов и несложных формул для нахождения тангенса в прямоугольном треугольнике. Мы же рассмотрим только некоторые из них.
Легче всего найти тангенс именно острого угла. Если даже это не угол прямоугольного треугольника, то дополнить его до прямоугольного не составит труда.
Это то, на чем построена сама сущность тангенса, но если нужно найти стороны, то это уже точно задача не про тангенсы.