арифметика с алгебраическими числами двоичные кода и операции с двоичными кодами
5. Арифметика с алгебраическими числами
5.1. Кодирование алгебраических чисел
Для представления чисел со знаком используются специальные коды:
Рис. 1. Формат представления числа
Поле знака представлено одним разрядом, в котором устанавливается 0, если число положительное, и 1, если число отрицательное.
Поле модуля отражает количественную оценку числа и для каждого кода формируется по-разному. Количество разрядов поля модуля определятся диапазоном изменения отображаемых чисел или точностью их представления.
В прямой код запись целого числа А формируется по следующему правилу:

В дополнительном коде запись целого числа А формируется по следующему правилу:

Для случая правильной дроби запись числа А в дополнительном коде имеет вид
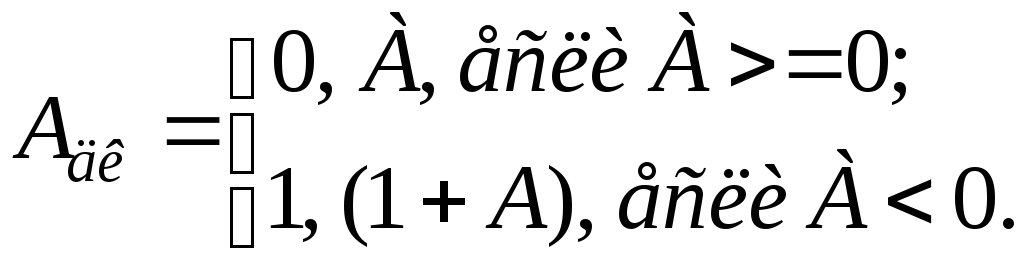
В обратном коде запись целого числа А формируется по следующему правилу:

Для случая правильной дроби запись числа В в обратном коде имеет вид

Легко показать, что перевод отрицательного числа из обратного или дополнительного кода в прямой выполняется по тому же правилу, что и перевод числа из прямого кода в обратный или дополнительный код: для того чтобы перевести отрицательное число из обратного в прямой код, необходимо дополнить его модуль до включенной границы; для того чтобы перевести отрицательное число из дополнительного в прямой код, необходимо дополнить его модуль до невключенной границы.
5.2. Логические операции с двоичными кодами
Над двоичными кодами могут выполняться различные логические операции, среди которых особое место занимают:
суммирование по модулю 2 (обозначается mod 2);
Операция логического суммирования выполняется над двумя кодами и генерирует код той же разрядности, что и операнды, у которого в некотором i-м разряде находится единица, если хотя бы в одном операнде в i-м разряде имеет место единица.
Операция логического умножения выполняется над двумя кодами и генерирует код той же разрядности, что и операнды, у которого в некотором i-м разряде находится единица, если оба операнда в этом i-м разряде имеются единицу, и ноль во всех других случаях.
Операция суммирования по модулю 2 выполняется над двумя кодами и генерирует код той же разрядности, что и операнды, у которого в некотором i-м разряде находится единица, если два заданных операнда в i-м разряде имеется противоположные значения. Иногда эта операция называется «исключающее ИЛИ».
Операция логического отрицания выполняется над одним кодом и генерирует результирующий код той же разрядности, что и операнд, у которого в некотором i-м разряде находится значение, противоположное значению в i-м разряде отрицаемого кода.
Сдвиг влево выполняется за счет установки в разряд значения, соответствующего исходному значению в ближайшем младшем разряде (освобождающийся самый правый т.е. самый младший, разряд заполняется 0, а «выталкиваемый» разряд пропадает). Например, код 11001110 после сдвига влево будет иметь вид 10011100.
Сдвиг вправо выполняется за счет установки в разряд значения, соответствующего исходному значению в ближайшем старшем разряде (в освобождающийся самый левый, т.е. самый старший, разряд заполняется 0, «выталкиваемый» разряд пропадает). Например, код 11001110 после сдвига влево будет иметь вид 01100111.
Арифметические сдвиги обеспечивают выполнения умножения (сдвиги влево) или операции деления (сдвиги вправо) двоичных кодов на два, точно так же, как сдвиги вправо и влево десятичного числа обеспечивают выполнение деления и умножение на 10.
Если сдвигается положительное число, то сдвиг (вправо или влево) выполняется как соответствующий логический сдвиг (влево или вправо), с той лишь разницей, что предусматриваются средства определения факта переполнения при сдвиге влево, что реализуется и при всех других арифметических операциях. При любом сдвиге вправо предусматриваются средства для округления после завершения нужного количества сдвигов и средства обнаружения обнуления сдвигаемой величины после очередного сдвига.
Арифметика с алгебраическими двоично-десятичными числами
Представление двоично-десятичных чисел в обратном и дополнительном кодах поясняется следующими примерами.
Найти дополнительный и обратный двоично- десятичный коды чисел
Двоично-десятичный код заданных чисел будет
А2-10 = 0110 1001 0001 0111,
Непосредственно используя правило формирования прямого, дополнительного и обратного кодов, найдем:
[Впк] = 1. 0010 1000 0100 0111,
— 0010 1000 0100 0111 = В2-10
Простое инвертирования модуля [В] пк дает значение [В] ик (инверсный код), равное
1101 0111 1011 1000,
которое отличается от требуемой формы модуля обратного кода тем, что каждая тетрада имеет избыточную шестерку. Обозначим такой код как «[B]ок+6».
Таким образом, модуль обратного кода двоично-десятичного числа не может быть сформирован из модуля прямого кода за счет инвертирования, как это имеет место в случае двоичного кода. Однако инвертирование при формировании обратного кода двоично-десятичного числа может быть использовано, если предварительно во все двоично-десятичные разряды (тетрады) ввести избыточную шестёрку. В этом случае для числа В имеет место:
При выполнении операций с алгебраическими двоично-десятичными числами на базе средств, реализующих двоичную арифметику, используется прием, согласно которому обработку чисел ведут по правилам двоичной арифметики с использованием ограниченного количества корректирующих операций, позволяющих получить искомый двоично-десятичный результат.
Данный подход иллюстрируется следующим примером.
Найти двоично-десятичные значения C1, C2, C3, C4, определяемых соответственно выражениями:
С1= А+В, С2=А-В, С3= В-А, С4=-А-В, используя модифицированный обратный код, если:
Результат представить в прямом коде. При реализации операции сложения использовать модифицированный обратный код.
Прямой двоично-десятичный код заданных чисел имеет вид
[А]пк = 0. 0011 0111 1000 0011,
[B] пк = 1. 0101 0100 1001 0010.
Расчет выражений для C1, C2, C3, C4 осуществляется следующим образом.
00. 0 0 1 1 0 1 1 1 1 0 0 0 0 0 1 1 [А]мок
+ 11. 1 0 1 0 1 0 1 1 0 1 1 0 1 1 0 1 [B] ик = [B]ок+6
11. 1 1 1 0 1 0 0 0 1 1 1 1 0 1 1 0
При выполнении первого суммирования по правилам двоичной арифметики возникающий перенос (в тетрадах, отмеченных знаком *) унес лишнюю 6 (двоичный перенос унес из тетрады 16, а по правилам десятичного сложения он должен унести 10), что означает, что избыточная «6», введенная за счет использования инверсного кода числа вместо обратного, исчезает в тех тетрадах, где был перенос, и сохраняется в тетрадах, где перенос отсутствовал. Коррекция на +6 выполняется в тех тетрадах, где был перенос. Таким образом после коррекции во всех тетрадах будет иметь место избыточная 6, что позволяет перейти от такой записи к прямому коду результата за счет инвертирования записей всех тетрад модульной части.
0 0. 0 0 0 1 1 1 0 1 0 0 0 0 1 1 1 1
При выполнении первого суммирования по правилам двоичной арифметики возникающий перенос (в тетрадах, отмеченных знаком *) унес лишнюю 6 (двоичный перенос унес из тетрады 16, а по правилам десятичного сложения он должен унести 10), что означает, что избыточная 6, введенная за счет использования инверсного кода числа вместо обратного, исчезает в тех тетрадах, где был перенос, и сохраняется в тетрадах, где перенос отсутствовал.
Формирование С2 и С3, в выражениях которых в операции сложения принимают участие числа с одинаковыми знаками, осуществляется за счет сложения абсолютных значений операндов с последующим присвоением полученной суммы знака одного из операндов.
Таким образом, для определения С2 и С3 выполняются следующие действия:
0 1000 1100 0001 0101
Таким образом, [С2] пк =0. 1001 0110 0111 0101, [С3] пк =
=1. 1001 0110 0111 0101.
Во всех примерах выполнения операций с использование прямого, дополнительного и обратного кода в качестве операндов рассматривались целые числа, т.е. точка, отделяющая целую от дробной части числа, предполагается расположенной после младшего разряда поля модуля записи числа. Для правильных дробей эта точка предполагается расположенной между полем знака и полем модуля. Как видно из приведенных примеров, ни при формировании заданного кода (прямого, дополнительного или обратного) на основании соответствующей записи числа, ни при выполнении операций с использованием этих кодов конкретное положение точки в записи числа не учитывалось. Поэтому формирование рассматриваемых кодов и их использование в случае дробных чисел ничем не отличаются от случая целых чисел.
Прямой, обратный и дополнительный коды двоичного числа
Прямой код двоичного числа
Обратный код двоичного числа
Дополнительный код двоичного числа

Мы знаем, что десятичное число можно представить в двоичном виде. К примеру, десятичное число 100 в двоичном виде будет равно 1100100, или в восьмибитном представлении 0110 0100. А как представить отрицательное десятичное число в двоичном виде и произвести с ним арифметические операции? Для этого и предназначены разные способы представления чисел в двоичном коде.
Сразу отмечу, что положительные числа в двоичном коде вне зависимости от способа представления (прямой, обратный или дополнительный коды) имеют одинаковый вид.
Прямой код
Обратный код
Для неотрицательных чисел обратный код двоичного числа имеет тот же вид, что и запись неотрицательного числа в прямом коде.
Для отрицательных чисел обратный код получается из неотрицательного числа в прямом коде, путем инвертирования всех битов (1 меняем на 0, а 0 меняем на 1).
Для преобразования отрицательного числа записанное в обратном коде в положительное достаточного его проинвертировать.
Арифметические операции с отрицательными числами в обратном коде:
Дополнительный код
В дополнительном коде (как и в прямом и обратном) старший разряд отводится для представления знака числа (знаковый бит).
Арифметические операции с отрицательными числами в дополнительном коде
Вывод:
1. Для арифметических операций сложения и вычитания положительных двоичных чисел наиболее подходит применение прямого кода
2. Для арифметических операций сложения и вычитания отрицательных двоичных чисел наиболее подходит применение дополнительного кода


Информатика. 8 класс
Система счисления – это совокупность правил для записи чисел.
Цифры – знаки, c помощью которых записываются числа.
Алфавит – множество всех цифр, используемых для записи чисел.
Система счисления называется позиционной, если количественный эквивалент цифры зависит от её положения (позиции) в записи числа.
Основание позиционной системы счисления равно количеству цифр, составляющих её алфавит.
Основанием позиционной системы счисления может служить любое натуральное число q > 1.
Алфавит десятичной системы состоит из десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Число, записанное в десятичной системе счисления, в развернутой форме записывается в виде суммы степеней 10 с коэффициентами-цифрами, используемыми в свернутой форме записи этого числа.
Сегодня мы познакомимся с двоичной системой счисления – позиционной системой счисления с основанием 2. Для записи чисел в двоичной системе счисления используются только две цифры: 0 и 1.
Рассмотрим перевод целых чисел, представленных в двоичном коде, в десятичную систему счисления.
Число, записанное в двоичной системе счисления, в развернутой форме записывается в виде суммы степеней двойки с коэффициентами-цифрами, используемыми в свернутой форме записи этого числа.
Такая форма записи «подсказывает» правило перевода натуральных двоичных чисел в десятичную систему счисления: необходимо вычислить сумму степеней двойки, соответствующих единицам в свёрнутой форме записи двоичного числа.
А теперь вы узнаете, как можно получить двоичный код (записать в двоичной системе счисления) любое целое десятичное число.
Для этого нужно последовательно выполнять деление данного числа и получаемых целых частных на два до тех пор, пока не получится частное, равное нулю.
Запись исходного числа в двоичной системе счисления составляется из полученных остатков, выписываемых последовательно справа налево.
Арифметика двоичной системы счисления основывается на использовании очень простых таблиц сложения и умножения, которым может позавидовать каждый первоклассник!
Арифметические операции в двоичной системе счисления осуществляются по тем же правилам, что и в десятичной системе счисления.
Рассмотрим операцию сложения.
В двоичной системе счисления один плюс один – это один-ноль, поэтому ноль остается в младшем разряде, а единица переносится в старший разряд.
Операция умножения в двоичной системе счисления сводится к сдвигам множителя и сложениям. Понаблюдайте, как это происходит, на примере.
Посмотрите, как происходит двоичное вычитание. При вычитании из нуля единицы занимаем единицу в старшем разряде.
Сегодня на уроке мы познакомились с двоичной системой счисления, научились переводить числа из двоичной системы счисления в десятичную и из десятичной системы счисления в двоичную.
Этих знаний и умений достаточно, чтобы объяснить секрет чудесной таблицы.
Вот так таблица будет выглядеть, если записать содержащиеся в ней числа в двоичной системе счисления.
В строке I записаны все числа, в двоичном изображении которых есть единицы первого разряда (1); в строке II записаны все числа, у которых есть единицы второго разряда (2); в строке III — числа, имеющие единицы третьего разряда (4), и в строке IV — числа, имеющие единицу четвертого разряда (8).
Если задуманное вами число есть, например, только в строках IV и II, то оно может быть представлено суммой 8 и 2. Следовательно, это 10.
Сегодня на уроке мы познакомились с двоичной арифметикой – узнали, как выполняются арифметические операции с двоичными числами. Вы убедились, что все происходит по тем же правилам, что и в привычной нам десятичной системе счисления.
Вся компьютерная техника построена на использовании двоичных кодов: с их помощью представляют, хранят, обрабатывают и передают по компьютерным сетям самые разные виды информации!
Арифметика с алгебраическими числами двоичные кода и операции с двоичными кодами
Сложение (вычитание). Операция вычитания приводится к операции сложения путем преобразования чисел в обратный или дополнительный код. Пусть числа A=>O и В=>О, тогда операция алгебраического сложения выполняется в соответствии с табл. 2.3.
Таблица преобразования кодов при алгебраическом сложении
Скобки в представленных выражениях указывают на замену операции вычитания операцией сложения с обратным или дополнительным кодом соответствующего числа. Сложение двоичных чисел осуществляется последовательно, поразрядно в соответствии с табл. 2.2. При выполнении сложения цифр необходимо соблюдать следующие правила. Классификация межсетевых экранов Курс лекций по информатике
1. Слагаемые должны иметь одинаковое число разрядов. Для выравнивания разрядной сетки слагаемых можно дописывать незначащие нули слева к целой части числа и незначащие нули справа к дробной части числа.
2. Знаковые разряды чисел участвуют в сложении так же, как и значащие.
3. Необходимые преобразования кодов (п.2.3.1) производятся с изменением знаков чисел. Приписанные незначащие нули изменяют свое значение при преобразованиях по общему правилу.
4. При образовании единицы переноса из старшего знакового разряда, в случае использования ОК, эта единица складывается с младшим числовым разрядом. При использовании ДК единица переноса теряется. Знак результата формируется автоматически, результат представляется в том коде, в котором представлены исходные слагаемые.
Исходные числа имеют различную разрядность, необходимо провести выравнивание разрядной сетки:
Сложение в обратном или дополнительном коде дает один и тот же результат
Обратим внимание, что при сложении цифр отсутствуют переносы в знаковый разряд и из знакового разряда, что свидетельствует о получении правильного результата.
Пример 2.10. Сложить два числа А10 = + 16 В10 = —7 в ОК и ДК. В соответствии с табл. 2.3 должна быть реализована зависимость А+(-В), в которой второй член преобразуется с учетом знака
При сложении чисел в ОК и ДК были получены переносы в знаковый разряд и из знакового разряда. В случае ОК перенос из знакового разряда требует дополнительного прибавления единицы младшего разряда (см.п.4 правил). В случае ДК этот перенос игнорируется.
Перемножим эти числа, представленные прямыми двоичными кодами, так же, как это делается в десятичной системе.
Нетрудно видеть, что произведение получается путём сложения частных произведений, представляющих собой разряды множимого, сдвинутые влево в соответствии с позициями разрядов множителя. Частные произведения, полученные умножением на нуль игнорируются. Важной особенностью операции умножения n-разрядных сомножителей является увеличение разрядности произведения до n+n=2n. Знак произведения формируется путём сложения знаковых разрядов сомножителей. Возможные переносы из знакового разряда игнорируются.
Деление. Операция деления, как и в десятичной арифметике, является обратной операции умножения. Покажем, что и эта операция приводится к последовательности операций сложения и сдвига.
Пример 2.12. Разделить два числа А10=45 B10 =5
Деление произведено так же, как это делается обычно в десятичной системе. Сначала проверяется, можно ли вычесть значение делителя из старших разрядов делимого. Если возможно, то в разряде частного записывается единица и определяется частная разница. В противном случае в частное записывается нуль и разряды делителя сдвигаются вправо на один разряд по отношению к разрядам делимого. К полученной предыдущей разнице сносится очередная цифра делимого, и данный процесс повторяется, пока не будет получена необходимая точность. Если учесть, что все вычитания в ЭВМ заменяются сложением в ОК или в ДК (см. табл.2.3), то действительно операция деления приводится к операциям сложения и сдвигам вправо разрядов делителя относительно разрядов делимого. Отметим, что делимое перед операцией деления должно быть приведено к 2n-разрядной сетке. Только в этом случае при делении на n-разрядный делитель получается n-разрядное частное.
Знак частного формируется также путем сложения знаковых разрядов делимого и делителя, как это делалось при умножении.
2.3.3. Арифметические операции над двоичными числами с плавающей точкой
В современных ЭВМ числа с плавающей точкой хранятся в памяти машин, имея мантиссу и порядок (характеристику) в прямом коде и нормализованном виде. Все арифметические действия над этими числами выполняются так же, как это делается с ними, если они представлены в полулогарифмической форме (мантисса и десятичный порядок) в десятичной системе счисления. Порядки и мантиссы обрабатываются раздельно.
Сложение (вычитание). Операция сложения (вычитания) производится в следующей последовательности.
1. Сравниваются порядки (характеристики) исходных чисел путем их вычитания р=р1-р2. При выполнении этой операции определяется, одинаковый ли порядок имеют исходные слагаемые.
2. Если разность порядков равна нулю, то это значит, что одноименные разряды мантисс имеют одинаковые веса (двоичный порядок). В противном случае должно проводиться выравнивание порядков.
3. Для выравнивания порядков число с меньшим порядком сдвигается вправо на разницу порядков Ар. Младшие выталкиваемые разряды при этом теряются.
4. После выравнивания порядков мантиссы чисел можно складывать (вычитать) в зависимости от требуемой операции. Операция вычитания заменяется операцией сложения в соответствии с данными табл. 2.3. Действия над слагаемыми производятся в ОК или ДК по общим правилам.
5. Порядок результата берется равным большему порядку.
6. Если мантисса результата не нормализована, то осуществляются нормализация и коррекция значений порядка.
В нормализованном виде эти числа будут иметь вид:
1. Вычитаем порядки Δp=p1-p2=1-0=1. В машине эта операция требует операции сложения с преобразованием порядка чисел в дополнительный код:
Определяем, что Δр≠ 0.
2. Порядок первого числа больше порядка второго числа на единицу. Требуется выравнивание порядков.
3. Для выравнивания порядков необходимо второе число сдвинуть вправо на один разряд.
4. Складываем мантиссы.
5. Порядок числа С равен порядку числа с большим порядком, т.е. р = +1.
Видно, что мантисса результата не нормализована, так как старшая цифра мантиссы равна нулю.
6. Нормализуем результат путем сдвига мантиссы на один разряд влево и соответственно вычитаем из значения порядка единицу:
Умножение (деление). Операция умножения (деления) чисел с плавающей точкой также требует разных действий над порядками и мантиссами. Алгоритмы этих операций выполняются в следующей последовательности.
1. При умножении (делении) порядки складываются (вычитаются) так, как это делается над числами с фиксированной точкой.
2. При умножении (делении) мантиссы перемножаются (делятся).
3. Знаки произведения (частного) формируются путем сложения знаковых разрядов сомножителей (делимого и делителя). Возможные переносы из знакового разряда игнорируются.


















